原文地址：Bitcoin

比特币：一种点对点电子现金系统

中本聪
congsatoshin@gmx.com
www.bitcoin.org

摘要本文提出了一种纯点对点版本的电子现金系统，它将允许一方直接将在线支付请求发送到另一方，而无需经过任何金融机构。数字签名部分解决了这个问题，但是如果仍然需要可信的第三方来防止双重支付/双重花费/双花(double-spending)，那么这个方案最重要的优点就没有了。我们提出了一个使用点对点网络来解决双重花费问题的方法。网络通过将交易散列到一个基于哈希的工作量证明(proof-of-work)的持续链中，形成一个记录，该记录在不重做工作量证明的情况下无法更改。最长的链不仅可以证明所发生交易的顺序，而且可以证明它来自最大的CPU算力池。只要CPU的大部分算力由不攻击这个网络的节点控制，它们就会产生最长的链，并超过攻击者。网络本身需要最小的结构。消息是在尽最大努力的基础上广播的，节点可以随意离开和重新加入网络，接受最长的工作量证明链，作为它们离开时发生的事情的证据。

1. 介绍 Introduction

　　电子商务已经几乎完全依赖金融机构作为可信的第三方来处理电子支付。虽然该系统对处理大多数交易都没有问题，但它仍然存在基于信任的模型的固有的弱点。完全不可逆的交易是不可能的，因为金融机构无法避免调解纠纷。调解成本增加了交易成本，限制了最小实际交易规模，并切断了小规模临时交易的可能性，而且，失去为不可逆服务支付不可逆款项的能力的代价更大。因为有潜在的退款的可能，就需要交易双方拥有信任。商家必须提防他们的顾客，顾客会向他们讨价还价，要求他们提供比他们需要的更多的信息。一定比例的欺诈被认为是不可避免的。这些成本和支付的不确定性可以通过用纸钞面对面交易，但是，在没有可信任的第三方的情况下，没有机制能够通过通信通道(communication channel)进行支付。

　　我们需要的是一个基于密码学的而不是基于信任的电子支付系统，允许任何两个自愿的当事方直接进行交易，而不需要可信的第三方。在计算上不可逆转的交易将保护卖方免受欺诈，而常规的第三方保管(escrew)机制可以很容易地实施来保护买方。在本文中，我们提出了一个解决双重花费问题的方法，使用一个点对点(peer to peer)的分布式时间戳服务器来生成交易的时间顺序的计算证明。只要诚实节点共同控制比任何一个攻击节点组更多的CPU算力，系统就是安全的。

2. 交易 Transactions

　　我们把电子货币定义为一系列数字签名。每个拥有者通过对前一次交易的哈希值和下一个所有者的公钥进行数字签名并将其添加到货币的末尾，从而将货币转移到下一个所有者。收款人可以验证签名以验证所有权链。

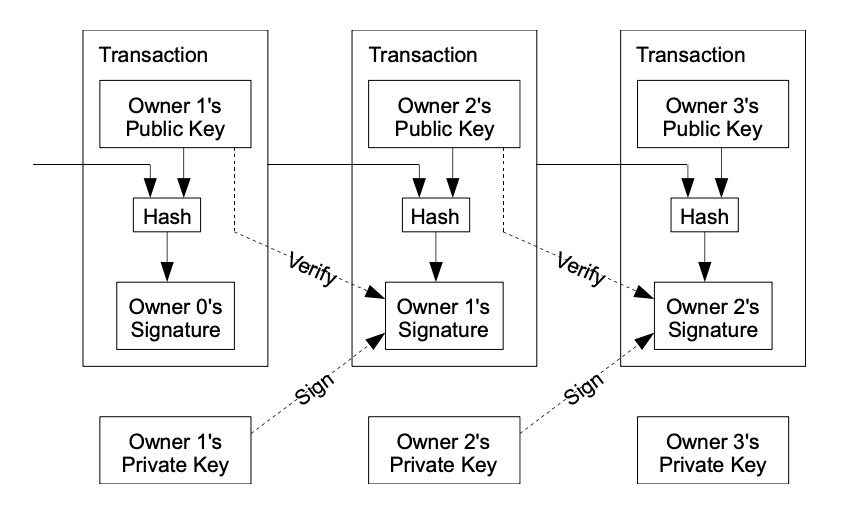
　　问题当然是受款人无法证实其中一个拥有者有没有双重花费这个货币。一个常见的解决方案是引入一个可信的中央机构或者是造币厂(mint)，它检查每一笔交易是否存在双重支出。每次交易后，必须将货币归还造币厂来发行新货币，只有直接从造币厂发行的货币才可被证实为没有被重复使用。这个解决方案的问题是，整个货币体系的命运取决于运营铸币厂的公司，每笔交易都必须经过它们，就像银行一样。

　　我们需要一种让收款人知道这个币之前的所有者未签署任何较早交易的方法。就我们的目的而言，最早的交易对我们来说有用，所以我们不在乎这之后的双重花费的尝试。确认没有交易有遗漏的唯一方法是了解所有交易。在以铸币厂为基础的模型中，铸币厂知道所有的交易，并决定哪个交易最先到达。为了在没有可信方的情况下实现这一点，交易必须公开宣布^[1]，我们需要一个系统，让参与者就其接收顺序的单一历史达成一致。受款人需要证明在每次交易时，大多数节点都同意它是第一次收到的。

3. 时间戳服务器 Timestamp Server

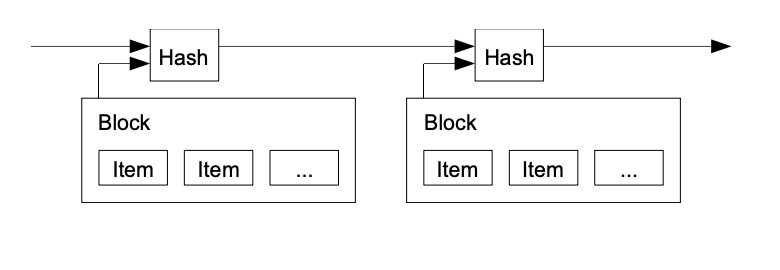
　　我们提出的解决方案从时间戳服务器开始。时间戳服务器的工作原理是获取要加时间戳的项目区块的哈希值并广泛地发布该哈希值，例如在报纸或Usenet帖子中^[2-5]。显然，为了进入散列，时间戳证明数据必须在当时已经存在。每个时间戳在其散列中包括前一个时间戳，形成一个链，每个附加的时间戳都加强前面的时间戳。

4. 工作量证明 Proof-of-Work

　　为了在点对点基础上实现分布式时间戳服务器，我们需要使用类似于Adam Back的Hashcash^[6]的工作量证明系统，而不是报纸或Usenet的帖子。工作量证明机制引入了对某一个特定值的扫描工作，比方说 SHA-256 下，随机散列值以一个或多个 0 开始。那么随着 0 的数目的上升, 找到这个解所需要的工作量将呈指数增长，但是检验结果仅需要一次随机散列运算。

　　我们在区块中补增一个随机数(Nonce)，这个随机数要使得该给定区块的随机散列值出现了所需的那么多个 0。我们通过反复尝试来找到这个随机数，找到为止。这样我们就构建了一个工作量证明机制。一旦CPU耗费的工作量使其满足工作量证明机制，那么除非重新完成相当的工作量，该区块的信息就不可更改。由于后面的区块被链接在它之后，更改这个区块的将重做它后面的所有区块。

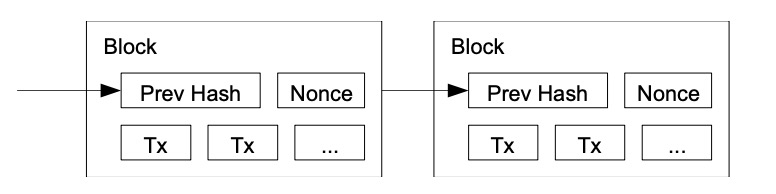
　　工作量证明还解决了在集体投票表决时，谁是大多数的问题。如果“大多数”是基于一个IP地址对应一次投票机会，那么那些能够获得多个IP的人就可以破坏这种“大多数”的公平性。工作量证明本质上是一个CPU对应一次投票机会。大多数决策是由最长的链来代表的，它有最大的工作量证明努力的投入。如果大部分CPU算力由诚实节点控制，则诚实链将增长最快，并超过任何竞争链。要修改一个过去的区块，攻击者必须重做该区块及其后所有区块的工作量证明，然后赶上并超越诚实节点的工作。稍后我们将说明，随着后续区块被添加，较慢的攻击者追赶的概率将呈指数下降。

　　为了补偿硬件速度的提高和对运行节点的兴趣随时间的变化，工作量证明的难度由针对每小时平均区块数的移动平均值确定。如果它们生成得太快，难度就会增加。

5. 网络 Network

运行这个网络的步骤如下：

1）新交易被广播到所有节点。

2）每个节点将新交易收集到一个区块中。

3）每个节点都为其区块找一个困难的工作量证明。

4）当一个节点找到工作量证明时，它将这个区块广播给所有节点。

5）只有当区块中的所有交易都有效且尚未花费时，节点才接受该区块。

6）节点通过使用接受的区块的散列作为前一个散列来创建链中的下一个区块，从而表达对区块的接受。

　　节点总是认为最长的链是正确的，并将继续扩展它。如果两个节点同时广播下一个区块的不同版本，则一些节点可能先接收其中一个。在这种情况下，它们处理接收到的第一个分支，但保存另一个分支以防它变长。当找到下一个工作量证明并且一个分支变长时，这种僵局(tie)将被打破；在另一个分支上工作的节点随后将切换到较长的分支。

　　新的交易广播不一定需要到达所有节点。只要它们到达许多节点，它们不久就会进入一个区块。区块广播也可以容忍丢弃的消息。如果一个节点没有接收到一个区块，在它收到下一个区块并意识到错过了一个区块时，它将请求这个丢失的区块。

6. 激励 Incentive

　　按照惯例，一个区块中的第一个交易是一个特殊的交易，它启动一个由区块创建者拥有的新货币。这增加了节点支持这个网络的动力，并提供了一种初始分配货币进入流通的方式，因为没有中央机构来发行货币。不断增加一定数量的新货币，类似于金矿商花费资源来增加黄金流通量。在我们的例子中，消耗的是CPU时间和电能。

　　激励也可以通过交易费(transcation fees)来资助。如果一项交易的输出值小于其输入值，则差额为交易费，该交易费将被加在包含该交易的区块的激励价值上。一旦预定数量的货币进入流通环节，这些激励可以完全转变为交易费用，完全不受通胀影响。

　　这种激励可能有助于鼓励节点保持诚实。如果一个贪婪的攻击者能够聚集比所有诚实的节点更多的CPU算力，他将不得不面临一个选择：使用这些算力来通过偷回他之前的付款，还是使用它来生成新的货币。他就会发现，遵守规则更有益于自己的利益，因为这种规则让他获得比其他人加起来更多的新货币，而不是破坏制度和他自己财富的有效性。

7. 回收磁盘空间 Reclaiming Disk Space

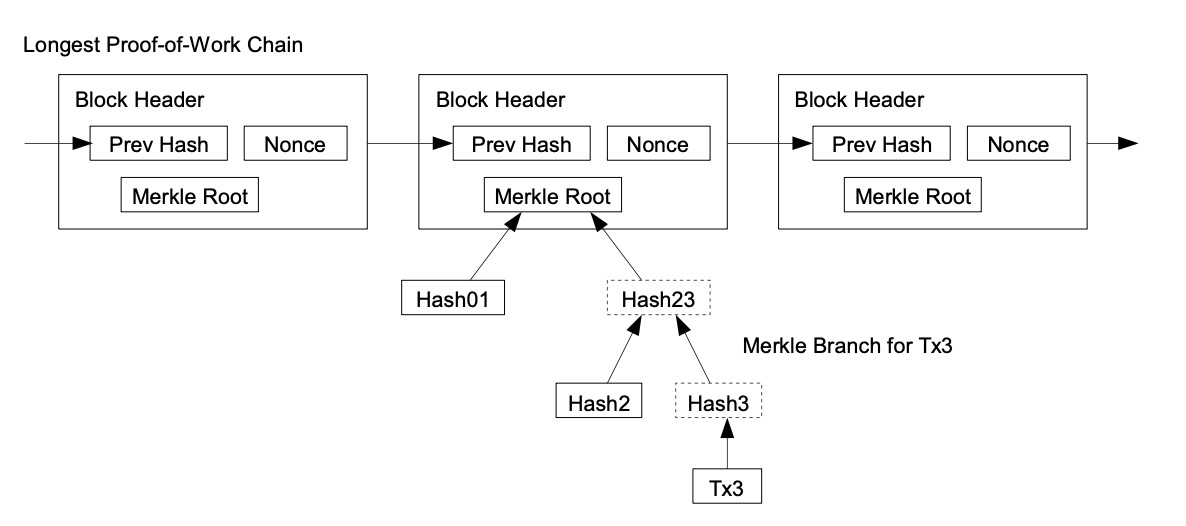
　　如果最近的交易已经被纳入了足够多的区块之中，那么就可以丢弃该交易之前的数据，以节省磁盘空间。为了同时确保不损害区块的随机散列值，交易信息被随机散列时，被构建成一种 Merkle 树^[7][2][5]的形态，使得只有根被纳入了区块的随机散列值。通过将该树的分支拔除(stubbing)的方法，老区块就能被压缩。而内部的随机散列值是不必保存的。

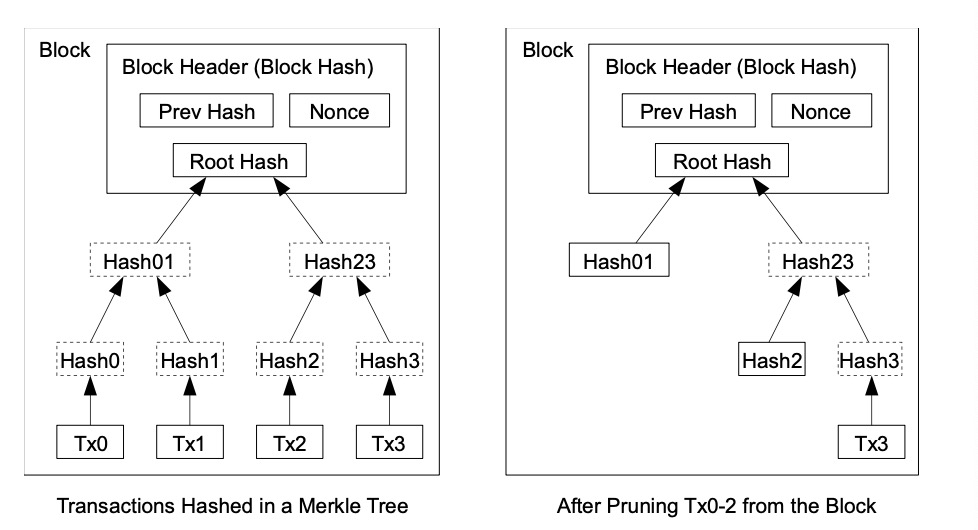
　　不含交易信息的区块头(block header)大约是80字节。如果我们假设每10分钟生成一次区块，80 bytes * 6 * 24 * 365 = 4.2 MB/年。2008年，计算机系统的RAM通常为2GB，而摩尔定律预测当前的年增长率为1.2GB，即使区块头必须保存在内存中，存储也不成问题。

8. 简化的支付验证 Simplified Payment Verification

　　可以在不运行完整网络节点的情况下验证支付。用户只需要保留最长的工作量证明链的区块头的副本，他可以通过查询网络节点，直到确信自己拥有最长的链，并获得将交易链接到其时间戳所在区块的Merkle分支。他无法亲自检查交易，但通过将交易链接到链中的某个位置，他可以看到网络节点已接受交易，并且，在它之后添加的区块进一步证实网络已经接受了交易。

　　因此，只要诚实的节点控制网络，验证就是可靠的，但如果网络被攻击者压倒，它就更容易受到攻击。虽然网络节点可以自己验证交易，但只要攻击者能够继续控制网络，简化的方法就会被攻击者捏造的交易欺骗。防范这种情况的一种策略是，当网络节点检测到无效区块时，接受来自它们的警报，提示用户的软件下载完整的区块并警告所有的交易以确认不一致性。频繁收到付款的企业可能仍希望运行自己的节点，以实现更独立的安全性和更快的验证。

9. 价值的组合与分割 Combining and Splitting Value

　　虽然可以单独处理货币，但要对转账中的每一分钱进行单独交易是不明智的。为了允许分割和组合价值，交易包含多个输入和输出。通常情况下，既有来自较大交易的单个输入，也有来自较小金额的多个输入，而且最多有两个输出：一个用于支付，另一个将找零（如果有的话）返回给发送方。

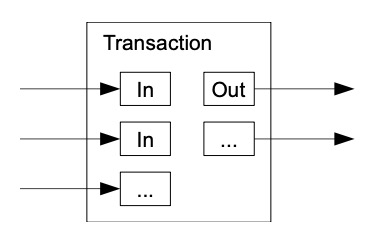
　　应该注意的是，扇出 (fan-out) (其中一个交易依赖于多个交易，而这些交易依赖于更多交易) 在这里不是问题。永远不需要提取交易历史的完整独立副本。

10. 隐私 Privacy

　　传统的银行模式通过限制相关方和可信的第三方能够访问的信息来达到一定程度的隐私。公开宣布所有交易的必要性否决了这种方法，但是隐私仍然可以通过在另一个地方破坏信息流来维护：通过保持公共密钥的匿名性。公众可以看到有人在向其他人发送金额，但没有信息将交易与任何人联系起来。这同证券交易所发布的信息是类似的，每一手交易发生的时间、交易量是记录在案且可供查询的，但是交易双方的身份信息却不予透露。

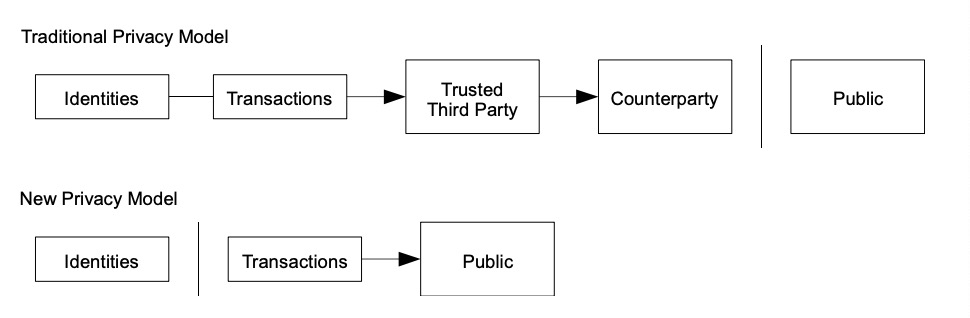
　　作为额外的预防措施，使用者可以让每次交易都生成一个新的地址，以确保这些交易不被追溯到一个共同的所有者。在多输入交易中，某些关联仍然是不可避免的，这必然表明它们的输入是由同一所有者拥有的。风险在于，如果密钥的所有者被泄露，链接可能会暴露属于同一所有者的其他交易。

11. 计算 Calculations

　　我们考虑攻击者试图以比诚实链更快的速度生成替代链的场景。即使实现了这一点，它也不会让系统能够被任意更改，例如凭空创造价值或从根本上拿走不属于攻击者的钱。节点不会接受无效的交易作为支付，诚实的节点永远不会接受包含它们的区块。攻击者只能尝试更改自己的一个交易，以收回他最近花的钱。

　　诚实链和攻击者链之间的竞争可以描述为二项随机漫步(Binomial Random Walk)。成功事件是诚实链被扩展一个区块，使其领先优势增加+1，而失败事件是攻击者的链被扩展一个区块，差距减少-1。

　　攻击者从给定的赤字中赶上的概率类似于赌徒的破产问题(Gambler’s Ruin Problem)。假设一个拥有无限信用的赌徒从亏损开始，并且可能进行无限次的尝试以达到盈亏平衡。我们可以计算出他达到盈亏平衡的概率，或者攻击者赶上诚实链的概率，如下^[8]：

p= 诚实节点找到下一个区块的概率

q = 攻击者找到下一个区块的概率

$q_z$=攻击者从后面z个区块追上来的概率 $\begin{gather} q_z = \begin{cases} 1 & if & p \leq q \\ (\frac{q}{p})^z & if & p>q \end{cases} \end{gather}$ 　　假设$p>q$，随着攻击者必须赶上的区块数的增加，概率呈指数级下降。在对他不利的情况下，如果他没有在早期幸运地向前冲，他的机会就会随着他落在后面而变得越来越小。

　　我们现在考虑新交易的接收者需要等待多长时间，才能充分确定发送方不能更改交易。我们假设发送者是一个攻击者，他想让接收者暂时相信他支付了他，并在一段时间后将支付转换为返还给自己。当这种情况发生时，接收者会得到提醒，但发送者希望这个提醒已经来不及了。

　　接收方生成一个新的密钥对，并在签名前不久将公钥交给发送方。这就阻止了发送者通过不断地处理一系列区块来提前准备区块链，直到他足够幸运地提前足够远，然后在那一刻执行交易。一旦交易被发送，不诚实的发送者就开始秘密地在一个包含其交易的备用版本的并行链上工作。

　　接收者等待，直到交易被添加到一个区块，并且在它之后链接了$z$个区块。他不知道攻击者的确切进度，但是假设诚实的区块占用了每个区块的平均预期时间，攻击者的潜在进度将是一个具有期望值的泊松分布： $\begin{gather} \lambda = z\frac{q}{p} \end{gather}$ 为了得到攻击者现在仍能赶上的概率，我们将他可能取得的每一个进步量的泊松密度乘以他从该点可以赶上的概率：

$\begin{gather} \sum_{k=0}^\infty\frac{\lambda^ke^{-\lambda}}{k!} = \begin{cases} (\frac{q}{p})^{(z-k)} & if & k \leq z \\ 1 & if & k>z \end{cases} \end{gather}$ 重新排列以避免对分布的无限尾部求和:

$\begin{gather} 1-\sum_{k=0}^z\frac{\lambda^ke^{-\lambda}}{k!}(1-(\frac{q}{p})^{(z-k)}) \end{gather}$ 转换为C代码:

#include <math.h>
double AttackerSuccessProbability(double q, int z) {
  double p = 1.0 - q;
  double lambda = z * (q / p); 
  double sum = 1.0;
  int i, k;
  for (k = 0; k <= z; k++){
    double poisson = exp(-lambda); 
    for (i = 1; i <= k; i++)
      poisson *= lambda / i;
      sum -= poisson * (1 - pow(q / p, z - k));
  }
  return sum; 
}

运行一些结果，我们可以看到概率随着$z$呈指数下降。

q=0.1
z=0 P=1.0000000 
z=1 P=0.2045873 
z=2 P=0.0509779 
z=3 P=0.0131722 
z=4 P=0.0034552 
z=5 P=0.0009137 
z=6 P=0.0002428 
z=7 P=0.0000647 
z=8 P=0.0000173 
z=9 P=0.0000046 
z=10 P=0.0000012

q=0.3
z=0 P=1.0000000 
z=5 P=0.1773523 
z=10 P=0.0416605 
z=15 P=0.0101008 
z=20 P=0.0024804 
z=25 P=0.0006132 
z=30 P=0.0001522 
z=35 P=0.0000379 
z=40 P=0.0000095 
z=45 P=0.0000024 
z=50 P=0.0000006

求解当$p$小于0.1%:

P < 0.001 
q=0.10 z=5 
q=0.15 z=8 
q=0.20 z=11 
q=0.25 z=15 
q=0.30 z=24 
q=0.35 z=41 
q=0.40 z=89 
q=0.45 z=340

12. 结论 Conclusion

　　我们提出了一个不需要信用中介的电子支付系统。我们从通常的数字签名货币框架开始，虽然这种系统为所有权提供了强有力的控制，但是不足以防止双重支付。为了解决这个问题，我们提出了一种使用工作量证明的点对点网络来记录交易的公共历史记录，如果诚实的节点控制了大部分CPU算力，则对于攻击者而言，更改记录很快就在计算上变得不切实际。该网络具有非结构化的简单性。节点之间的工作大部分是彼此独立的，只需要很少的协同。它们不需要被标识，因为消息不会被路由到任何特定的地方，只需要在尽最大努力的基础上进行传递。节点可以随意离开和重新加入网络，接受工作量证明链作为它们离开时发生了什么的证据。他们用自己的CPU算力投票，通过扩展有效区块来表达他们对有效区块的接受，通过拒绝处理无效区块来拒绝这些区块。任何必要的规则和激励措施都可以通过这种协商一致机制来执行。

引用 References

[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.

[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.

[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no2, pages 99-111, 1991.

[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,” In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.

[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference on Computer and Communications Security*, pages 28-35, April 1997.

[6] A. Back, “Hashcash - a denial of service counter-measure,”http://www.hashcash.org/papers/hashcash.pdf, 2002.

[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.

[8] W. Feller, “An introduction to probability theory and its applications,” 1957.

COMMENT BOARD

「翻译」Bitcoin

Bitcoin: A Peer-to-Peer Electronic Cash System 逐字翻译